提醒：本页面将不再更新、维护或者支持，文章、评论所叙述内容存在时效性，涉及技术细节或者软件使用方面不保证能够完全有效可操作，请谨慎参考！

原创文章，未经允许，请勿转载！

关系型数据库一般都是以平面方式来存储我们的数据，这就造成了我们在实现一些数据结构上的麻烦，比如说如何实现高效的无限级的网站分类，这里MySQL的 《Managing Hierarchical Data in MySQL》 给出了一个比较好的办法，基于一种左右值的算法，这也是我目前接触到的 查询比较高效 的算法了，另外Gijs Van Tulder在sitepoint也写过一篇 《Storing Hierarchical Data in a Database》 文章专门讲解这个算法，我在这里再总结一下，首先看下面的这张图：

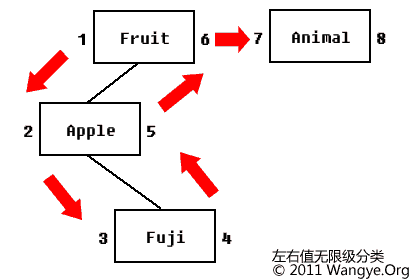
通过这张图大家应该能很清晰的看出对于一种简单的树形结构分类的左右值处理的方式，这是一种类似于树的深度优先的遍历，其次这些左右权值很清晰的表明了一种隶属的包含关系，比如Fruit的左右值分别为1~6，那么说，所有在这个之间的值都是其子节点(Child Node)。对于数据库的遍历，我们可以很轻松的指定一个范围，然后执行一条SELECT查询语句。

下面我就先增加做个讲解，假设数据表的结构如下：

+-------------+-----------------+
| name        | type            |
+-------------+-----------------+
| ID          | INT AUTOINC     |
| Name        | VARCHAR     	|
| PID         | INT             |
| LeftValue   | INT             |
| RightValue  | INT             |
+-------------+-----------------+

首先ID表示节点的唯一ID标识，Name表示节点的名称，PID表示所继承的父节点ID，LeftValue和RightValue顾名思义分别代表了左右值，由这些可以知道我们可以通过ID和Name的值定位到一个节点，当然这里的前提是Name必须是唯一的，否则我们只能使用ID来定位，在下面的讲解中，我将只采用ID的方式定位一个节点。

我在这里用 伪码 将一些操作总结一下，假设以this代表这张关系表，假设我们插入一个节点，节点的右值始终大于节点的左值，对于表空的情况来说，右值比左值大1个单位。那么简单的插入函数可以像下面这样表示：

function insertNode(value) 
{ 
  left = value + 1; 
  right = value + 2; 
  this.insert(left, right);  
}

这里很明显，如果表为空，那么value就为0，然后我们就插入了第一个节点，可能有童鞋要问，value是神马东东？下面的讲解中我将告诉你。

当插入第二个节点时，问题就来了，我们遇到了三个问题，第一是这时插入分为两种情况，同级节点和子级节点，第二个问题是如果得到自身的左右权值，第三个问题是先前插入的节点权值要发生改变，是的，但是是怎样的改变法呢？不着急，让我们先看第一个问题，第一个问题很好解决，我们分两种情况讨论就可以了，先讨论第一种情况同级节点插入(Same level node insert)，什么是同级关系，所谓的同级关系也就是说是同等级的节点，该节点与被插入位置的节点是并列关系，也就是说是邻居节点(Neighbours’Node)。比如我们希望插入节点后结构图变成这样：

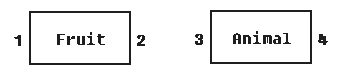
原先表中只有Fruit，后来插入了Animal，那么Animal和Fruit就是一种并列关系，接下来让我们看下第二个问题，如何知道自身的左右值？再回到刚才讲解insertNode(value)这个地方，嘿，这时我们的value发挥作用了，它给我们提供了一个基准，首先大家发现任何一个叶子节点的右值减去左值都得到1，这个是必然的，也是我们insertNode函数里面的+1和+2的由来，那么如何得到value这个基准值呢？你可以试着将这张图拓展一下，然后多列出一些同级节点，然后就像我那样画出箭头，然后用手指优雅的划一下，然后你就会发现，第一次访问到我们新插入的同级节点是从该节点的左边第一个同级节点访问到的，这句话比较讲，这样吧，我们看图，比如说Animal是我们后插入的，那么根据箭头，我们第一次访问到Animal这个节点时是从Fruit这个节点过来的，Fruit是Animal的第一个左节点，同样的你会发现一个规律，计数也恰巧从Fruit的右值开始，6、7、8，难道是巧合，这不是巧合，你多试几次就能发现规律，那么我们的基准值value也很明显了，那就是所有同级节点（不包括待插入节点）的右值的最大值，下面我们要直面第三个问题，Fruit的值要改变？要改变吗？不需要！那么第三个问题不需要管了么，答案是否定的，大家发现每个节点的左值小于新插入节点的左值时说明该节点左值没有越界，所以不需要更新，同样的，每个节点的右值小于新插入节点的左值时也说明不需要更新，那么什么情况下需要更新呢？让我们先看图：

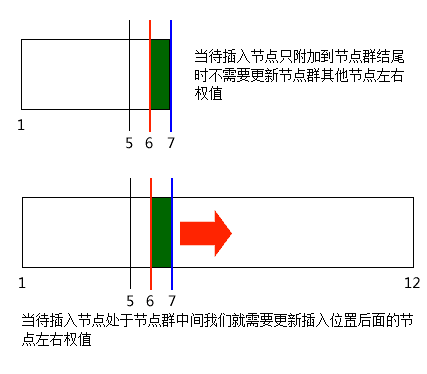
从图中不难看出先前我们的插入属于结尾附加，所以不需要更新任何节点，然而当节点树比较复杂时，有可能会出现中间新插入的现象，那么我们就有必要更新所有插入之后的节点的左右数值了，更新的基准是什么？更新多少？从上图大家可能会发现，我们插入的节点所赋予的新的左右权值为6和7，如果插入位置位于段中的话，那么势必要占去原节点群6和7这两个权值，是的，所有大于5的都要向后挪，具体挪几个，刚才已经说，占去的只是6和7两个权值，那么就是要挪2个位置，即在原有的权值的基础上增加2，判断的基准就是5，5是什么，想必大家能够猜到，5就是前面我讲的insertNode(value)的value基准值。

基于上面的论点，首先我们来看段根据指定的基准条件进行权值增加的伪码算法：

function addAllNodeValues(new_left, new_right, fn_compare) 
{ 
  while(this = this.next) { 
    left = this.node.left; 
    right = this.node.right; 
    if (fn_compare(left)) 
        left = left + new_left; 
    if (fn_compare(right)) 
        right = right + new_right; 
    this.update(left, right); 
  } 
}

上述算法中，new_left是新增加的左值，new_right为新增加的右值，注意，这里是指在原有的基础上进行加权，fn_compare是个回调函数，返回true是才进行加权，这个回调函数仅一个参数，即遍历所有节点所获得的左（右）的权值。下面改进过的插入同级节点的算法如下：

function insertSameLevelNode(parent_id) 
{ 
  // 如果找不到就返回0 
  value = this.nodes(parentId == parent_id).rights.maxValue; 
  addAllNodeValues(2, 2, function(cmp_value){return (cmp_value > value)}); 
  insertNode(value); 
}

到这里同级节点插入已经讲解完了，接下来将要谈谈子节点的插入，我们回到文章开始的那幅图，假设Fruit节点下插入Apple，根据上面同级节点的插入同理可知，Apple这个节点的左右值是基于Fruit的左值得到的，大家可以看箭头的方向，那么value基准值即为Fruit的左值。同样的我们仍然需要判断value是否越界，判断的方式和上面一样，综合来看得到算法如下：

function insertChildNode(parent_id) 
{
  // 因为父节点是唯一的，所以只要获取第一个左值即可
  value = this.nodes(id == parent_id).lefts[0]; 
  addAllNodeValues(2, 2, function(cmp_value){return (cmp_value > value)}); 
  insertNode(value); 
}

至此，关于插入节点的算法已经讲解完毕！